load(os.environ['SAGE_STARTUP_FILE'])
|
|
Sage는 대수적 계산을 할수있는 프로그램(Computer Algebra System (CAS))으로 무료로 sagemath.org 에서 다운로드하여 설치 할 수 있다. 웹서버를 인터페이서로 사용하며 브라우저를 통해 접속하여 사용하기 때문에 인터넷이되는 모든 장소에서 이용할 수 있다. 세이지의 기본언어는 객체지향 언어인 파이썬(Python)이며 이를 사용하여 프로그래밍도 할 수 있다. http://sage.kunsan.ac.kr 에 접속하여 계정을 만들고 사용한다.
대수(Algebra)
2+3
|
|
2-3
-1 -1 |
2*3
6 6 |
1.5/5
0.300000000000000 0.300000000000000 |
|
|
2^3
8 8 |
2**3
8 8 |
2^(-3)
1/8 1/8 |
인수분해
factor(100215)
3^2 * 5 * 17 * 131 3^2 * 5 * 17 * 131 |
전개하기
a,b=var('a,b') #변수를 처음 도입할때 선언을 한다. 주의: #뒤의 모든것은 무시된다. 또는 아래와 같이
|
|
u,v=var('u,v') #same as u,v=var('u,v')
|
|
expand((a+b)^10)
|
|
방정식 해 구하기
solve(x^2-3*x+1==0,x) #방정식을 나타낼 때 == 을 사용함에 주의.
[x == -1/2*sqrt(5) + 3/2, x == 1/2*sqrt(5) + 3/2] [x == -1/2*sqrt(5) + 3/2, x == 1/2*sqrt(5) + 3/2] |
a=2
|
|
solve(x^3-3*x^2-x+3==0,x)
[x == 1, x == -1, x == 3] [x == 1, x == -1, x == 3] |
연립방정식
y=var('y') #변수 y를 도입하자
|
|
solve([x-y==3,x+y==5],x,y)
[[x == 4, y == 1]] [[x == 4, y == 1]] |
함수 (Function): 함수정의는 아래 두가지 방법을 사용하여 할 수 있다.
f(x)=x*sin(x)
|
|
f(1.0)
0.841470984807897 0.841470984807897 |
다음은 파이썬 방법이다.
def k(x):
a=x*sin(x)
return a
|
|
|
|
def h1(x,y)
return x**2+2*x*y+(x+y)**10
|
|
h1(1,2)
Traceback (click to the left of this block for traceback) ... NameError: name 'h1' is not defined Traceback (most recent call last):
File "<stdin>", line 1, in <module>
File "_sage_input_24.py", line 10, in <module>
exec compile(u'open("___code___.py","w").write("# -*- coding: utf-8 -*-\\n" + _support_.preparse_worksheet_cell(base64.b64decode("aDEoMSwyKQ=="),globals())+"\\n"); execfile(os.path.abspath("___code___.py"))
File "", line 1, in <module>
File "/tmp/tmpx6lPgV/___code___.py", line 3, in <module>
exec compile(u'h1(_sage_const_1 ,_sage_const_2 )
File "", line 1, in <module>
NameError: name 'h1' is not defined
|
def h(x,y):
a=x**2+2*x*y+(x+y)**10
return a
|
|
# e^(x+y)
def g(x,y):
return exp(x+y)
|
|
g(1,1)
e^2 e^2 |
h(1,3.1)
1.34227313101524e6 1.34227313101524e6 |
미분(Differentiation)
$\frac{d}{dx} k(x)$
simplify(diff(sin(x),x,1)-cos(x))
0 0 |
|
|
$\frac{d}{dx} f(x)$
diff(sin(x),x,1)-cos(x)
0 0 |
$\frac{d}{dx} \sin(x)$
diff(cos(x),x,20)-cos(x)
0 0 |
y=var('y')
|
|
편미분(Partial Differentiation)
$\frac{\partial}{\partial x} \sin(x y)$
y=var('y')
|
|
diff(sin(x*y),x)
y*cos(x*y) y*cos(x*y) |
diff(sin(x*y),y,10).subs(x=1,y=1).n()
-0.841470984807897 -0.841470984807897 |
$\frac{\partial^2}{\partial x^2} \sin(x y)$
diff(sin(x*y),y)
Traceback (click to the left of this block for traceback) ... NameError: name 'y' is not defined Traceback (most recent call last):
File "<stdin>", line 1, in <module>
File "_sage_input_21.py", line 10, in <module>
exec compile(u'open("___code___.py","w").write("# -*- coding: utf-8 -*-\\n" + _support_.preparse_worksheet_cell(base64.b64decode("ZGlmZihzaW4oeCp5KSx5KQ=="),globals())+"\\n"); execfile(os.path.abspath("___code___.py"))
File "", line 1, in <module>
File "/tmp/tmpfot9cH/___code___.py", line 2, in <module>
exec compile(u'diff(sin(x*y),y)
File "", line 1, in <module>
NameError: name 'y' is not defined
|
$\frac{\partial^3}{\partial x \partial y^2} \sin(x y)$
diff(sin(x*y),y,20,x)
x^20*y*cos(x*y) + 20*x^19*sin(x*y) x^20*y*cos(x*y) + 20*x^19*sin(x*y) |
diff(sin(x*y),x,y)
-x*y*sin(x*y) + cos(x*y) -x*y*sin(x*y) + cos(x*y) |
위 예제에서 편미분이 미분 순서에 무관함을 보이시오.
적분(Integration)
$\int k(x) dx$
ff=integral(k(x),x)
Traceback (click to the left of this block for traceback) ... NameError: name 'k' is not defined Traceback (most recent call last):
File "<stdin>", line 1, in <module>
File "_sage_input_28.py", line 10, in <module>
exec compile(u'open("___code___.py","w").write("# -*- coding: utf-8 -*-\\n" + _support_.preparse_worksheet_cell(base64.b64decode("ZmY9aW50ZWdyYWwoayh4KSx4KQ=="),globals())+"\\n"); execfile(os.path.abspath("___code___.py"))
File "", line 1, in <module>
File "/tmp/tmpTaLj37/___code___.py", line 2, in <module>
exec compile(u'ff=integral(k(x),x)
File "", line 1, in <module>
NameError: name 'k' is not defined
|
ff
-x*cos(x) + sin(x) -x*cos(x) + sin(x) |
diff(ff,x)
x*sin(x) x*sin(x) |
$\int_1^2 k(x) dx$
k(x)=e^-x^2
|
|
integral(k(x),x,0,1) #정적분
1/2*sqrt(pi)*erf(1) 1/2*sqrt(pi)*erf(1) |
위의 결과를 소수로 나타내기 위해서는 함수 $n()$을 점(.)으로 덧붙이면 된다 (객체지향 언어의 특성).
integral(k(x),x,0,1).n()
0.746824132812427 0.746824132812427 |
|
|
수치 적분(Numerical integration)
$\int_0^\pi \sin(x)^2 dx$ 를 수치계산과 정확한 계산으로 구해보고 비교해 보자. 두 계산 결과가 오차범위내에서 일치함을 주목하라.
numerical_integral(cos(x^2),0,3) #수치계산. 앞의 수가 결과를 나타내며 두번째 수는 오차를 나타내며 e-14는 10^(-14)를 의미한다.
|
|
integral(sin(x)^2,x,0,pi) #정확한(exact) 계산. 이경우 적분변수 (x)를 표시함에 주의 하시오.
1/2*pi 1/2*pi |
1.5707963267948966192 1.5707963267948966192 |
$\int_0^\infty e^{-\sqrt{x}} dx$
|
|
f=exp(-x^2)
|
|
f
e^(-x^2) e^(-x^2) |
integral(exp(-x^2),x,-infinity,infinity)
|
|
numerical_integral(f,-infinity,Infinity) #Infinity는 무한대를 나타내는 기호. 대문자로 시작함에 주의.
(1.7724538509055137, 3.429548872025538e-08) (1.7724538509055137, 3.429548872025538e-08) |
integral(f,x,0, Infinity)
2 2 |
numerical_integral(sin(f),0,pi)
(1.0226025498810094, 6.629450086680393e-07) (1.0226025498810094, 6.629450086680393e-07) |
plot(sin(cos(x)),x,0,pi)
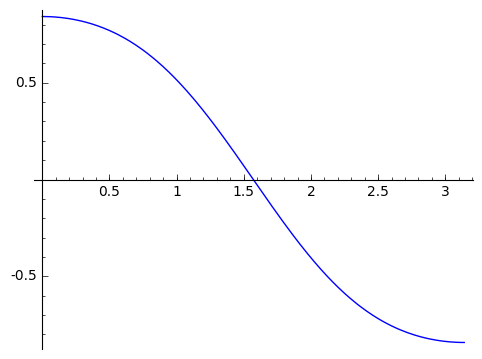
|
numerical_integral(sin(f),0,pi)
(1.0226025498810094, 6.629450086680393e-07) (1.0226025498810094, 6.629450086680393e-07) |
plot(exp(sin(x)),x,0,100)
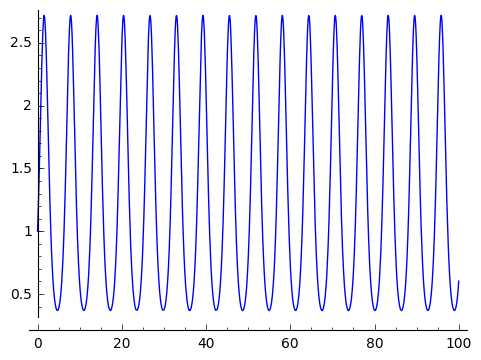
|
대입(substitution)
k(x).subs(x=2)
2*sin(2) 2*sin(2) |
k(x)=x*sin(x)
|
|
a,b=var('a,b')
|
|
g=(a^2+b^2)/a/b
|
|
g.subs(a=1,b=2)
5/2 5/2 |
y=var('y')
|
|
a=x^2+y^3+2*x*y
|
|
a
y^3 + x^2 + 2*x*y y^3 + x^2 + 2*x*y |
a.subs(x=2,y=1.5)
13.3750000000000 13.3750000000000 |
k(2)
2*sin(2) 2*sin(2) |
diff(k(x),x).subs(x=2)
2*cos(2) + sin(2) 2*cos(2) + sin(2) |
diff(k(x),x).subs(x=2).n() # x=2에서의 k(x)의 기울기
0.0770037537313969 0.0770037537313969 |
실수값얻기
pi #원주율
pi pi |
pi.n(digits=100)
3.1415926535897932384626433832795028841971693993751058209749445923078164\ 06286208998628034825342117068 3.141592653589793238462643383279502884197169399375105820974944592307816406286208998628034825342117068 |
a,b=var('a,b')
|
|
f1=(a+b)^5/(a^2*b^3)
|
|
f1.subs(a=3,b=2)
|
|
k(2).n()
|
|
k(2).n(digits=40) #정확도를 지정할 때
1.818594853651363390792039731823489685405 1.818594853651363390792039731823489685405 |
List (데이터 저장과 처리에 매우 중요)
a,b,c,d,e=var('a,b,c,d,e') #변수 선언
|
|
L1=[a,b,3]
|
|
L1
[a, b, 3] [a, b, 3] |
len(L1) #리스트의 원소 갯수, length
3 3 |
L1.append(c) #list에 원소를 추가할때
|
|
L1
[a, b, 3, c] [a, b, 3, c] |
L1.append(d); L1
[a, b, 3, c, d] [a, b, 3, c, d] |
L1
[a, b, 3, c, d] [a, b, 3, c, d] |
L1.remove(b) #원소 b를 제거
|
|
L1
[a, 3, c, d] [a, 3, c, d] |
|
|
L1.remove(d); L1
[a, 3, c] [a, 3, c] |
L1[0];L1[1];L1[2]# 리스트의 원소를 뽑아보자.원소를 지칭하는 인덱스는 0에서 시작함을 주의한다.
a 3 c a 3 c |
L1[2]
c c |
l2=[9,-1,2,-3,5,2,7]
|
|
l2[0]*l2[6]
|
|
l2.sort() #l2를 순서대로 정렬
|
|
l2.reverse()
|
|
l2
|
|
range(10) #파이썬 내장 정수 리스트
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9] [0, 1, 2, 3, 4, 5, 6, 7, 8, 9] |
range(20)
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19] [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19] |
range(2,10)
[2, 3, 4, 5, 6, 7, 8, 9] [2, 3, 4, 5, 6, 7, 8, 9] |
range(11,30)
[11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29] [11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29] |
range(2,20,3)
[2, 5, 8, 11, 14, 17] [2, 5, 8, 11, 14, 17] |
range(1,50,3)
[1, 4, 7, 10, 13, 16, 19, 22, 25, 28, 31, 34, 37, 40, 43, 46, 49] [1, 4, 7, 10, 13, 16, 19, 22, 25, 28, 31, 34, 37, 40, 43, 46, 49] |
srange(2,3,0.1) #세이지 내장 리스트의 하나
[2.00000000000000, 2.10000000000000, 2.20000000000000, 2.30000000000000, 2.40000000000000, 2.50000000000000, 2.60000000000000, 2.70000000000000, 2.80000000000000, 2.90000000000000] [2.00000000000000, 2.10000000000000, 2.20000000000000, 2.30000000000000, 2.40000000000000, 2.50000000000000, 2.60000000000000, 2.70000000000000, 2.80000000000000, 2.90000000000000] |
import numpy #numpy 수치계산 패키지를 불러들인다
|
|
numpy.arange(2,10,0.1) #0.1 단위로 원소가 증가 함을 주의
array([ 2. , 2.1, 2.2, 2.3, 2.4, 2.5, 2.6, 2.7, 2.8, 2.9, 3. ,
3.1, 3.2, 3.3, 3.4, 3.5, 3.6, 3.7, 3.8, 3.9, 4. , 4.1,
4.2, 4.3, 4.4, 4.5, 4.6, 4.7, 4.8, 4.9, 5. , 5.1, 5.2,
5.3, 5.4, 5.5, 5.6, 5.7, 5.8, 5.9, 6. , 6.1, 6.2, 6.3,
6.4, 6.5, 6.6, 6.7, 6.8, 6.9, 7. , 7.1, 7.2, 7.3, 7.4,
7.5, 7.6, 7.7, 7.8, 7.9, 8. , 8.1, 8.2, 8.3, 8.4, 8.5,
8.6, 8.7, 8.8, 8.9, 9. , 9.1, 9.2, 9.3, 9.4, 9.5, 9.6,
9.7, 9.8, 9.9])
array([ 2. , 2.1, 2.2, 2.3, 2.4, 2.5, 2.6, 2.7, 2.8, 2.9, 3. ,
3.1, 3.2, 3.3, 3.4, 3.5, 3.6, 3.7, 3.8, 3.9, 4. , 4.1,
4.2, 4.3, 4.4, 4.5, 4.6, 4.7, 4.8, 4.9, 5. , 5.1, 5.2,
5.3, 5.4, 5.5, 5.6, 5.7, 5.8, 5.9, 6. , 6.1, 6.2, 6.3,
6.4, 6.5, 6.6, 6.7, 6.8, 6.9, 7. , 7.1, 7.2, 7.3, 7.4,
7.5, 7.6, 7.7, 7.8, 7.9, 8. , 8.1, 8.2, 8.3, 8.4, 8.5,
8.6, 8.7, 8.8, 8.9, 9. , 9.1, 9.2, 9.3, 9.4, 9.5, 9.6,
9.7, 9.8, 9.9])
|
-----------------------------------------------------------
그래프
k(x)=cos(x**2)
|
|
plot(k(x),x,0,3,figsize=5)
Traceback (click to the left of this block for traceback) ... NameError: name 'k' is not defined Traceback (most recent call last):
File "<stdin>", line 1, in <module>
File "_sage_input_21.py", line 10, in <module>
exec compile(u'open("___code___.py","w").write("# -*- coding: utf-8 -*-\\n" + _support_.preparse_worksheet_cell(base64.b64decode("cGxvdChrKHgpLHgsMCwzLGZpZ3NpemU9NSk="),globals())+"\\n"); execfile(os.path.abspath("___code___.py"))
File "", line 1, in <module>
File "/tmp/tmpiNXNjd/___code___.py", line 3, in <module>
exec compile(u'plot(k(x),x,_sage_const_0 ,_sage_const_3 ,figsize=_sage_const_5 )
File "", line 1, in <module>
NameError: name 'k' is not defined
|
plot(k(x)*sin(10*x),x,0,10,color='green',figsize=5) # x-축 영역 지정
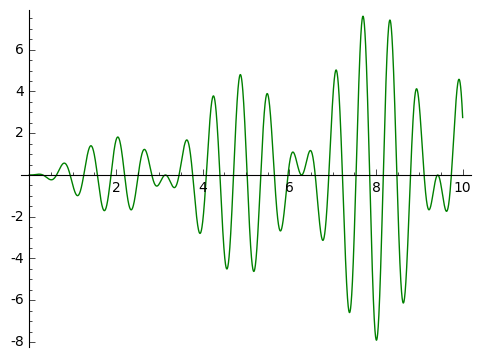
|
한 그림창에 여러개 그리기
plot(k(x)*sin(10*x),x,0,10)+plot(k(x),x,0,10, color='red')+plot(k(x)*sin(20*x),x,0,10,color='green',figsize=5) #동시에 그릴때는 + 를 사용한다.
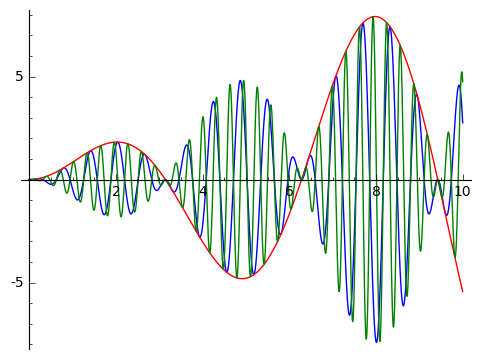
|
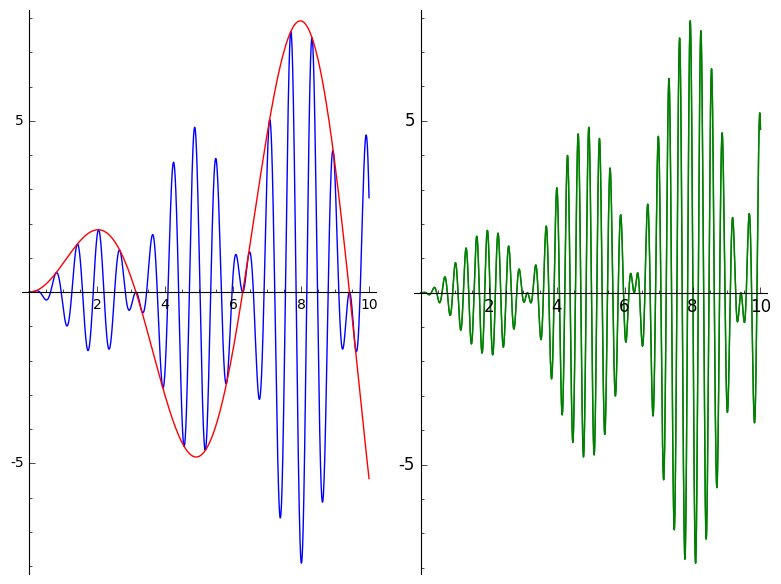
여러개 그림창을 동시에 그리기
fig1=plot(k(x)*sin(10*x),x,0,10)+plot(k(x),x,0,10, color='red')
fig2=plot(k(x)*sin(20*x),x,0,10,color='green',figsize=5)
graphics_array((fig1,fig2))
|
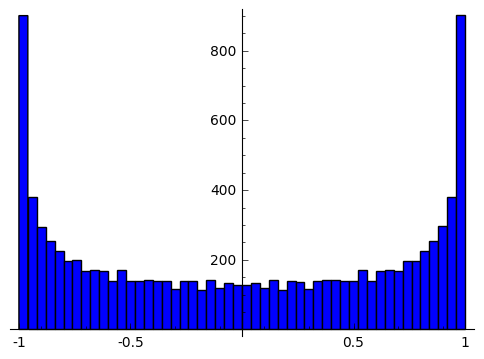
히스토그램
h_data=[sin(i) for i in range(10000)] #데이타셑을 만들자
histogram(h_data,bins=50,figsize=5)
|
y=var('y')
|
|
g=exp(-x^2-2*y^2)
|
|
plot3d(g,(x,-5,5),(y,-5,5))
|
|
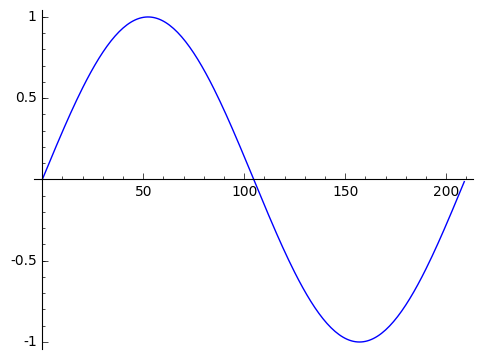
l2=[sin(0.3*i) for i in srange(0,21,0.1)] #l2의 원소는 range(21) 안의 모든 원소를 i에 대입하여 얻어진다.
|
|
cos(x**2)
|
|
list_plot(l2,plotjoined=True,figsize=5) #점들을 연결해 보자.
|
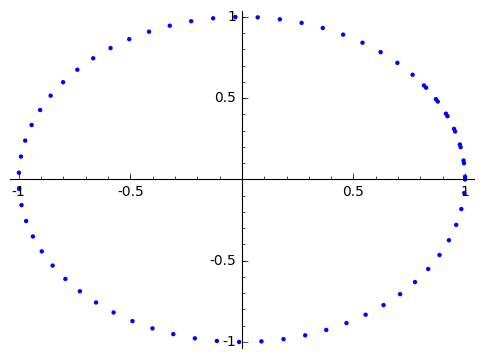
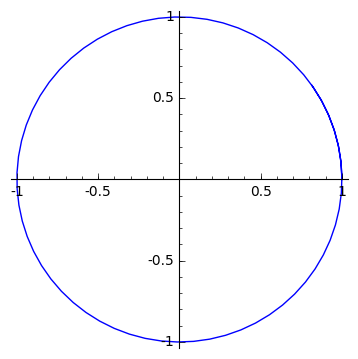
l5=[(cos(0.1*i),sin(0.1*i)) for i in range(70)] # range(20)안의 모든 원소를 i에 대입하여 리스트를 만든다.
|
|
list_plot(l5,figsize=5)
|
list_plot(l5,aspect_ratio=1,plotjoined=True ,figsize=5) #x, y축의 비율을 조절하기 위해서는 aspect_ratio를 사용한다.
|
3D List Plot
#Generate some 3D data
a=2.0
w=1.5
data=[]
for t in srange(0,15,0.1):
data.append((a*cos(w*t),a*sin(w*t),t))
|
|
list_plot(data,plotjoined=True)
|
|
-------------------------------------------------------------------------
선형대수 (Linear Algebra)
u=vector([1,2,3]) #List가 벡터함수의 input임을 주의
|
|
u
(1, 2, 3) (1, 2, 3) |
v=vector([-1,3,5]);v
(-1, 3, 5) (-1, 3, 5) |
u.dot_product(v) #내적
20 20 |
u.cross_product(v) #외적
(1, -8, 5) (1, -8, 5) |
v.cross_product(u) #외적의 순서를 바꾸면 부호가 바뀐다.
(-1, 8, -5) (-1, 8, -5) |
M=matrix([[1,2,3],[2,5,6],[-1,0,3]]);M #행렬함수도 리스트를 받아들임을 주의
[ 1 2 3] [ 2 5 6] [-1 0 3] [ 1 2 3] [ 2 5 6] [-1 0 3] |
M*u
(14, 30, 8) (14, 30, 8) |
u*M
(2, 12, 24) (2, 12, 24) |
M.inverse() #역행렬을 구한다.
[ 5/2 -1 -1/2] [ -2 1 0] [ 5/6 -1/3 1/6] [ 5/2 -1 -1/2] [ -2 1 0] [ 5/6 -1/3 1/6] |
iM=M.inverse()
|
|
M*iM
[1 0 0] [0 1 0] [0 0 1] [1 0 0] [0 1 0] [0 0 1] |
iM*M
[1 0 0] [0 1 0] [0 0 1] [1 0 0] [0 1 0] [0 0 1] |
M.det() #determinant 를 구한다.
6 6 |
S=matrix([[1,2,3],[2,1,4],[3,4,5]]);S #S는 대칭행렬
[1 2 3] [2 1 4] [3 4 5] [1 2 3] [2 1 4] [3 4 5] |
S.det()
8 8 |
ev=S.eigenvalues();ev #S의 고유값. 대칭행렬의 고유값은 실수임을 유의.
[-1.486979759027261?, -0.592545608423468?, 9.07952536745073?] [-1.486979759027261?, -0.592545608423468?, 9.07952536745073?] |
K=S.eigenvectors_right();K #고유벡터.
[(-1.486979759027261?, [(1, -7.323700036494775?, 4.053473437987430?)], 1), (-0.592545608423468?, [(1, -0.11487917829899307?, -0.4542624172751605?)], 1), (9.07952536745073?, [(1, 1.188579214793769?, 1.900788979287731?)], 1)] [(-1.486979759027261?, [(1, -7.323700036494775?, 4.053473437987430?)], 1), (-0.592545608423468?, [(1, -0.11487917829899307?, -0.4542624172751605?)], 1), (9.07952536745073?, [(1, 1.188579214793769?, 1.900788979287731?)], 1)] |
u1=K[0][1];u1 #u1은 K의 첫번째 고유값에 대응하는 고유벡터를 추출한다.
[(1, -7.323700036494775?, 4.053473437987430?)] [(1, -7.323700036494775?, 4.053473437987430?)] |
v1=u1[0];v1 #u1은 원소가 하나인 리스트이고 그 원소가 바로 고유 벡터이다.
(1, -7.323700036494775?, 4.053473437987430?) (1, -7.323700036494775?, 4.053473437987430?) |
S*v1/ev[0] #이것이 바로 v1임을 주의해 보시오.
(1.000000000000000?, -7.323700036494775?, 4.053473437987430?) (1.000000000000000?, -7.323700036494775?, 4.053473437987430?) |
*********두번째와째 세번째 고유값에 대해서도 같은 연습을 해보시오.*************
-------------------------------------------------------------------------
프로그래밍
For-loop (반복할때)
s=0
for i in range(1,11):
s=s+i
print s
1 3 6 10 15 21 28 36 45 55 1 3 6 10 15 21 28 36 45 55 |
s=0
for i in range(0,5001,2):
s=s+i
print s
6252500 6252500 |
p=1
for i in [1,2,3,5]: #list 안의 모든 원소을 차례로 곱한다.
p=p*i
print p
30 30 |
p=1
for k in range (1,11):
p=p*k
print p
3628800 3628800 |
p=1
for i in range(1,101,2):
p=p*i
print p
272539213975072950298071324540091863329079633054580341373432882344310620\ 1171875 2725392139750729502980713245400918633290796330545803413734328823443106201171875 |
동시에 합과 곱을 계산해 보자
s=0
p=1
q=0
for i in range (1,10): #range 가 1에서 시작. 즉, 1,2,3,...9
s=s+i #인덴트가 있는데까지 loop 이 적용됨.
p=p*i
q=q+i**2
print s,p,q #인덴트가 없으므로 loop 에서 빠져 나옴.
print '합=',s,',', '그리고','product=',p #문자는 따옴표속에.
45 362880 285 합= 45 , 그리고 product= 362880 45 362880 285 합= 45 , 그리고 product= 362880 |
함수를 사용해 보자
def sumprod(x,y):
return x+y, x*y
def main():
a=2
b=3
sum,prod=sumprod(a,b)
print '합=',sum,',','곱=',prod
main()
합= 5 , 곱= 6 합= 5 , 곱= 6 |
ex) List 의 원소의 갯수를 헤아려 보자
count=0
mm=[1,2,5,6,777,5,2,100]
for i in mm:
count=count+1 #loop 속에서 인덱스 i 를 쓰지 않아도 됨을 주의 하라.
print count
8 8 |
len(mm)
8 8 |
count=0
mk=range(1,1000000,7)
for i in mk:
count=count+1
print count
142857 142857 |
ex) 1에서 1000사이의 홀수의 합을 계산해 보자
s=0
for i in range(1,1000,2): #range 는 1에서 시작하여 2만큼 999까지 간다. 즉, 1,3,5,7,....,999
s=s+i
print s
250000 250000 |
s=0
for i in range(1,100,2):
s=s+i**3
print s
12497500 12497500 |
mm=[3,5,2,-1,6,9]
s=0
for i in range(5):
s=s+mm[i]*mm[i+1]
print s
71 71 |
s=0
for i in range(1,1001):
s=s+1/i
print s
533629132822947850455910456240429804096524722803842600971013492484562688\ 894971017575060979019850356914090887315504680983784421721178850094643023\ 443265660225021002784256328520814055449412104425101426727702947747127089\ 179639677796104532246924268664688882815820719848971051107968732493191555\ 293970175089315645199760857344730141832840117244122806490743077037366831\ 700558002936592350885893602352858528081607595747378366554131755081315225\ 17/712886527466509305316638415571427292066835886188589304045200199115432\ 408758111149947644415191387158691171781701957525651298026406762100925146\ 587100430513107268626814320019660997486274593718834370501543445252373974\ 529896314567498212823695623282379401106880926231770886197954079124775455\ 804932647573782992335275179673524804246363805113703433121478174685087845\ 348567802188807537324992199567205693202909939089168748767269795093160352\ 0000 53362913282294785045591045624042980409652472280384260097101349248456268889497101757506097901985035691409088731550468098378442172117885009464302344326566022502100278425632852081405544941210442510142672770294774712708917963967779610453224692426866468888281582071984897105110796873249319155529397017508931564519976085734473014183284011724412280649074307703736683170055800293659235088589360235285852808160759574737836655413175508131522517/7128865274665093053166384155714272920668358861885893040452001991154324087581111499476444151913871586911717817019575256512980264067621009251465871004305131072686268143200196609974862745937188343705015434452523739745298963145674982128236956232823794011068809262317708861979540791247754558049326475737829923352751796735248042463638051137034331214781746850878453485678021888075373249921995672056932029099390891687487672697950931603520000 |
s.n()
7.48547086055035 7.48547086055035 |
응용: 적분
L=3.141597/2
h=L/10000
area=0
for i in range(10000):
area=area+h*sin(h*i)
print area
0.999923631223926 0.999923631223926 |
L=pi.n()/4
h=L/100000
int=0
for i in range(100000):
int=int+h*tan(h*i)
print int
0.346569663294292 0.346569663294292 |
integral(tan(x),x,0,pi/4).n()
0.346573590279973 0.346573590279973 |
If 조건문 (경우를 따질때)
lst=[-3,-1,-2,0,1,2,3,4]
for i in lst:
if i<0:
print i, ':a negative number'
elif i==0: #같은지 아닌지를 따질때 == 사용
print i, ':a zero'
else:
print i, ':a positive number'
-3 :a negative number -1 :a negative number -2 :a negative number 0 :a zero 1 :a positive number 2 :a positive number 3 :a positive number 4 :a positive number -3 :a negative number -1 :a negative number -2 :a negative number 0 :a zero 1 :a positive number 2 :a positive number 3 :a positive number 4 :a positive number |
s=0
N=1000000
up=3.0
low=0.0
h=(up-low)/N
x=low
while x <=up:
aa=h*cos(x**2)
s=s+aa
x=x+h
print s.n()
0.702863691057069 0.702863691057069 |
lst=[-1,-2,0,1,2,3,-1,7,9,5,6]
for i in lst:
if i<0:
print i, ':a negative number' #elif 나 else 는 선택사항이지 필수가 아니다.
-1 :a negative number -2 :a negative number -1 :a negative number -1 :a negative number -2 :a negative number -1 :a negative number |
s=0
for i in range(1,256):
if i%3==0:
elif i%5==0:
s=s+i
print s
Traceback (click to the left of this block for traceback) ... SyntaxError: invalid syntax Traceback (most recent call last): print s
File "", line 1, in <module>
File "/tmp/tmpnDP8L3/___code___.py", line 6
elif i%_sage_const_5 ==_sage_const_0 :
^
SyntaxError: invalid syntax
|
|
|
|
|
s=0
for i in lst:
if i>0:
s=s+i
print s
33 33 |
s=0
for a in lst:
if 1<=a<=5:
s=s+a
print s
11 11 |
s=0
for a in lst:
if 1<=a:
if a<=5:
s=s+a
print s
11 11 |
위 리스트의 음수의 합을 구해보라.
Logical Operators
# AND, OR
MM=[-1,2,-3,-5,0,0,2,3,4,7,11,12]
n1=0
n2=0
for i in MM:
if i<0 or i>7:
print 1, i
for i in MM:
if i>0 and i<10:
print 2,i
1 -1 1 -3 1 -5 1 11 1 12 2 2 2 2 2 3 2 4 2 7 1 -1 1 -3 1 -5 1 11 1 12 2 2 2 2 2 3 2 4 2 7 |
While loop (조건이 맞을때까지 무한 반복)
s=0
i=0
while s<1000: #조건이 만족하는한 반복해서 계산한다.
i=i+1
s=s+i
print i-1,s-i
44 990 44 990 |
s=0
for i in range(100):
s=s+i
if s>=1000:
break
print i-1,s-i
44 990 44 990 |
if X%Y=0
|
|
s=0
for i in range(45):
s=s+i
print s
990 990 |
s1=0
j=0
while s1<10000:
j=j+1
s1=s1+j
print j-1,s1-i
140 9967 140 9967 |
|
|
For-loop 에서 빠져나오기 (break)
합이 1000을 넘지 않을때까지 더해보자
s=0
for i in range(1000000):
s=s+i
if s>1000:
print i-1,s-i
break #loop 에서 빠져나온다.
44 990 44 990 |
s=0
for i in range(45):
s=s+i
print s
990 990 |
Defining a function recursively (순환으로 함수 정의하기)
#factorial 함수를 정의해 해보자.
def nfactorial(n):
if n==0:
return 1
else:
return n*nfactorial(n-1)
|
|
for i in range(6):
print i,nfactorial(i)
0 1 1 1 2 2 3 6 4 24 5 120 0 1 1 1 2 2 3 6 4 24 5 120 |
#factorial 함수를 while loop 을 사용하여 정의해 보자.
def nfacto(n):
if n==0:
return 1
else:
p=n
i=n
while i>1:
i=i-1
p=p*i
return p
|
|
nfacto(3); nfacto(5)
6 120 6 120 |
def myabs(n):
if n>0:
print n
else:
print -n
|
|
myabs(3)
3 3 |
myabs(-5)
5 5 |
def facto(n):
if n<0:
print 'Give a positive number'
else:
p=1
for i in range(1,n+1):
p=p*i
return p
|
|
facto(4)
24 24 |
facto(-100)
Give a positive number Give a positive number |